How To Long Divide Polynomials
Dividing Polynomials
Dividing polynomials is an arithmetic operation where we divide a polynomial by another polynomial, generally with a lesser caste equally compared to the dividend. The division of ii polynomials may or may not result in a polynomial. Allow'south learn about dividing polynomials in this commodity in detail.
| 1. | What is Dividing Polynomials? |
| 2. | Dividing Polynomials by Monomials |
| three. | Dividing Polynomials by Binomials |
| 4. | Dividing Polynomials Using Synthetic Partitioning |
| five. | FAQs on Dividing Polynomials |
What is Dividing Polynomials?
Polynomials are algebraic expressions that consist of variables and coefficients. Information technology is written in the post-obit format: 5x2 + 6x - 17. This polynomial has three terms that are bundled according to their degree. The term with the highest degree is placed first, followed past the lower ones. Dividing polynomials is an algorithm to solve a rational number that represents a polynomial divided by a monomial or some other polynomial. The divisor and the dividend are placed exactly the same way as we do for regular division. For example, if we need to split up 5xii + 7x + 25 past 6x - 25, nosotros write information technology in this way:
\[\dfrac{(5 x ^2+7 x+25)}{(6 x -25)}\]
The polynomial written on top of the bar is the numerator ( 5xii + 7x + 25), while the polynomial written below the bar is the denominator (6x - 25). This can be understood by the following figure which shows that the numerator becomes the dividend and the denominator becomes the divisor.
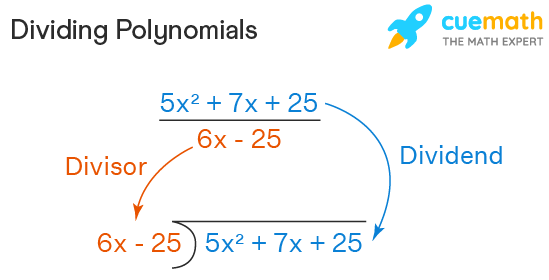
Dividing Polynomials past Monomials
While dividing polynomials by monomials, the partitioning can be washed in two means. One is by simply separating the '+' and '-' operator signs. That ways, we break the polynomial from the operating sign, and solve each part separately. Some other method is to do the simple factorization and farther simplifying. Permit u.s.a. have a look at both methods in detail.
Splitting the Terms Method
Split the terms of the polynomial separated by the operator ( '+' or '-' ) between them and simplify each term. For case, (4x2 - 6x) ÷ (2x) can exist solved every bit shown here. We first take common terms from the numerators and denominators of both the terms, we get, [(4xii) / (2x)] - [(6x) / (2x)]. Canceling the common term 2x from the numerator and the denominator, nosotros get 2x - iii.
Factorization Method
When yous divide polynomials yous may accept to factor the polynomial to detect a common gene between the numerator and the denominator. For example: Divide the following polynomial: (2xii + 4x) ÷ 2x. Both the numerator and denominator accept a common factor of 2x. Thus, the expression tin be written as 2x(10 + 2) / 2x. Canceling out the common term 2x, we get 10+2 as the respond.
Dividing Polynomials by Binomials
For dividing polynomials past binomials or any other type of polynomials, the most mutual and general method is the long division method. When there are no mutual factors between the numerator and the denominator, or if y'all can't discover the factors, you can use the long division procedure to simplify the expression.
Dividing Polynomials Using Long Division
Allow us go through the algorithm of dividing polynomials by binomials using an example: Divide: (4x2 - 5x - 21) ÷ (x - three). Hither, (4x2 - 5x - 21) is the dividend, and (x - 3) is the divisor which is a binomial. Find the segmentation shown beneath, followed by the steps.
Step i. Split up the kickoff term of the dividend (4x2) by the first term of the divisor (x), and put that as the first term in the quotient (4x).
Step ii. Multiply the divisor past that answer, place the product (4x2 - 12x) beneath the dividend.
Step 3. Subtract to create a new polynomial (7x - 21).
Step four. Repeat the same procedure with the new polynomial obtained after subtraction.
So, when we are dividing a polynomial (4x2 - 5x - 21) with a binomial (x - 3), the quotient is 4x+7 and the residuum is 0.
Dividing Polynomials Using Synthetic Sectionalisation
Synthetic division is a technique to divide a polynomial with a linear binomial past simply considering the values of the coefficients. In this method, we offset write the polynomials in the standard course from the highest caste term to the everyman degree terms. While writing in descending powers, use 0'due south as the coefficients of the missing terms. For case, x3+three has to be written every bit teniii + 0xii + 0x + 3. Follow the steps given below for dividing polynomials using the synthetic segmentation method:
Let us divide x2 + iii by x - four.
Step one: Write the divisor in the form of x - grand and write 1000 on the left side of the division. Here, the divisor is x-4, so the value of grand is iv.
Step ii: Set the division past writing the coefficients of the dividend on the right and k on the left. [Note: Use 0's for the missing terms in the dividend]
Step 3: Now, bring downwards the coefficient of the highest degree term of the dividend as it is. Here, the leading coefficient is 1 (coefficient of xtwo).
Step 4: Multiply k with that leading coefficient and write the production below the second coefficient from the left side of the dividend. And then, we become, iv×1=4 that we will write below 0.
Footstep five: Add the numbers written in the second column. Hither, past adding nosotros get 0+4=iv.
Step 6: Repeat the aforementioned procedure of multiplication of k with the number obtained in step 5 and write the product in the adjacent column to the right.
Stride 7: At last, we will write the final answer which will exist one caste less than the dividend. Then, here, in our dividend, the highest caste term is x2, therefore, in the caliber, the highest degree term volition be x. Therefore, the answer obtained is x+four+(nineteen/x-four).
Topics Related to Dividing Polynomials
Bank check these articles to know more about the concept of dividing polynomials and its related topics.
- Long division of polynomials
- Synthetic division of polynomial
- Partition Algorithm for Polynomials
- Dividing Ii Polynomials
- Division of Polynomial by Linear Factor
Dividing Polynomials Examples
-
Case 1: Alex is stuck on a problem while working on dividing polynomials. Tin you assistance him to obtain the quotient: (xfour - 10xiii + 27xii - 46x + 28) ÷ (ten - 7).
Solution:
Therefore, the quotient is x3 - 3x2 + 6x - four.
-
Case 2: Stacy needs help in finding the remainder while dividing polynomials. Can y'all aid her solve this?
(4xiii + 5xtwo + 5x + 8) ÷ (4x + 1)
Solution: Using the long segmentation method of dividing polynomials, nosotros get,
Therefore, the residual is 7.
become to slidego to slide
Have questions on basic mathematical concepts?
Get a problem-solving gnaw using logic, not rules. Acquire the why behind math with our certified experts
Book a Free Trial Class
Practice Questions on Dividing Polynomials
go to slidego to slide
FAQs on Dividing Polynomials
What is Dividing Polynomials?
Dividing polynomials is one of the arithmetic operations performed on two given polynomials. In this, the dividend is mostly of a higher degree and the divisor is a lower degree polynomial.
Why is Dividing Polynomials Important?
Dividing polynomials is important because it provides an algorithm to solve a rational number that represents a polynomial divided by a monomial or some other polynomial.
What is the Easiest Fashion for Dividing Polynomials?
The easiest way to divide polynomials is past using the long division method. Still, in the instance of the partition of polynomials by a monomial, it can be direct solved by splitting the terms or past factorization.
What are the Two Methods of Dividing Polynomials?
The two methods to divide polynomials are given below:
- Synthetic segmentation method
- Long division method
What is Polynomial Division Used for in Real-Life?
We use polynomial division for various aspects of our mean solar day-to-day lives. We need it for coding, engineering, designing, architecting, and various other real-life areas.
What Method of Dividing Polynomials by a Monomial is All-time?
In the case of the sectionalization of polynomials past a monomial, it can be directly solved by splitting the terms or by factorization. We can separate each term of the dividend with the given monomial and notice the consequence.
Source: https://www.cuemath.com/algebra/dividing-polynomials/
Posted by: robinsonmishated.blogspot.com
0 Response to "How To Long Divide Polynomials"
Post a Comment